مقدمة للجسم الصلب

   لماذا ندرس فيزياء الجسم الصلب (المادة الكثيفة)؟

    لأنها تشكل معظم الكون من حولنا , تقريباً كل الكون الذي نراه هو في الواقع مادة كثيفة

بدراسة الجسم الصلب نستطيع الاجابة عن الكثير من التساؤلات مثل:

لماذا تلمع المعادن؟ ولماذا الزجاج شفاف؟ ولماذا الماء سائل ويسبب الرطوبة؟

و لماذا المطاط املس و مرن (قابل للتمدد)؟ ......

كل هذه التساؤلات نجيب عنها و نفهمها بدراسة الجسم الصلب

وأحد أهم الطرق لدراسة الجسم الصلب هي دراسة البنية البلورية للجسم الصلب

وهذه الطريقة تهتم بشكل أساسي بطريقة توضع ذرات المادة ضمن الفراغ الذي تشغله هذه المادة و بنوع هذه الذرات .

لا بد لدراسة  البنى البلورية ان نتعرف على عدة مصطلحات :
1- شبكة برافيه  bravais lattice
2- خلية الوحدة الأولية primitive unit cell
3-الخلية الاصطلاحية  conventional unit cell
4-خلية وينر-زايتس الأولية   wigner-seitz primitive cell

1- شبكة برافيه bravais lattice

هي مجموعة لا نهائية من النقاط المنفصلة و التي تكون متوضعة بطريقة منظمة و بتوجيه معين بحيث ان هذه المجموعة من النقاط تبدو بنفس الشكل بغض النظر من اي نقطة ننظر لها

و يمكن أن نصيغ تعريف رياضي مكافئ لهذا التعريف :

في الشبكة ثلاثية الأبعاد كل النقاط في الشبكة يكون لها موضع يتحدد بالمتجه R

:ثلاث متجهات لا على التعيين و لكن لا تقع في نفس المستوي(متجهات أولية)

                      و لا يقطع المتجه الأولي سوى نقطة واحدة من الشبكة 

أعداد صحيحة ( موجب أو سالب أو صفر)

• في حال شبكة ذات بعدين يكون

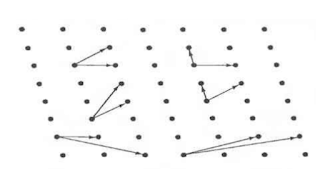يبين هذا الشكل عدة خيارات لاختيار الأشعة الاولية لنفس الشبكة وكل هذه الخيارات متكافئة

• وفي حال شبكة ببعد واحد يكون

يبين هذا الشكل شبكة ببعد واحد و شبكة ببعدين و شبكة بثلاث ابعاد

أذاً الشبكة يجب أن تحقق شرطين لتكون من شبكات برافيه :

1-   التنظيم(الترتيب) :  توزع منظم لنقاط الشبكة

2-   التوجه :  أن تكون الشبكة بنفس المنظر (الشكل) من كل النقاط المشكلة للشبكة

اي ان يكون التوجه و التنظيم نفسه بحيث اذا نظرنا من أي نقطة من الشبكة نرى نفس الترتيب (التنظيم و التوجه) أي نفس المنظر بالضبط

يبين الشكل السابق شبكة برافييه ذات بعدين و قد تم اختيار اشعة اولية لا على التعيين 

هما a1 و a2

لاحظ انه يجب ان يحقق هذين الشعاعين شرط الانسحاب اي ان الشعاع المحصل

  

يحدد موضع كل نقاط الشبكة و ذلك باعطاء قيم صحيحة للثوابت 

مثلاً  للحصول على النقطة p نضع 

وبالمثل النقطة Q يكون متجه الموضع لها 

ويمكن تعميم نفس المناقشة على الشبكة ثلاثية الابعاد.

    إن كون شبكات برافيه لا نهائية ينجم في الحقيقة من الشرط أن كل النقاط يجب أن تكون متكافئة (نفس التوجه و الترتيب)

بعبارة اخرة ان تكون كل النقاط متطابقة ولا يمكن التمييز بينها

مثلا في الشكل السابق النقطة T تكافئ تماما النقطة O  حيث كل منهما لديه نفس الجوار

(اي نفس عدد النقاط بجانب كل منهما و بنفس البعد و الاتجاه)

اما النقطة P   مثلاً لا يوجد نقطة فوقها و بالتالي لا تطابق النقطة T  ولكن ذلك ينجم عن اننا لم نكمل رسم الشبكة و بالتالي يوجد نقاط تمتد للانهاية و من هنا ياتي شرط برافييه ان الشبكة يجب ان تكون لانهائية.

و لكن في الواقع البلورات منتهية و لكن أذا كانت البلورة كبيرة بما يكفي نعتبرها غير منتهية(تقريب)

اذاً شبكة برافيه لها ثلاث معاني متكافئة:

1-   مجموعة نقاط لا نهائية

2-   الاشعة (أشعة الموضع للنقاط)

3-   مجموعة الانتقالات للشعاع R من نقطة إلى أخرى

  2- خلية الوحدة الأولية   primitive unit cell

    (ندعوها اختصاراً خلية الواحدة أو الخلية الأولية)

لا يوجد طريقة مميزة لاختيار خلية الواحدة

يوجد عدة خلايا وحدة للشبكة

الخلية الأولية يجب ان تحوي نقطة واحدة فقط من الشبكة (عقدة واحدة)

هذا يؤدي إلى انه إذا كان n   هو كثافة النقاط في الشبكة وكان    حجم الخلية الأولية

 نجد: 

أي  : 

من هذه النتيجة نتوصل الى أنه من أجل أي خلية أولية نختارها لشبكة ما يكون الحجم (حجم هذه الخلية) مستقل عن طريقة اختيارنا لهذه الخلية الأولية

اذاً الخلية الاولية: هي حجم من الفضاء بحيث عندما ينتقل هذا الحجم وفق كل المتجهات في شبكة برافيه يملأ كل الفضاء بدون أن يتداخل هذا الحجم مع نفسه وبدون ترك أي فراغات.

• يبين الشكل التالي عدة خيارات ممكنة للخلية الاولية من أجل نفس الشبكة في بعدين:

 لاحظ أن كل خلية من هذه الخلايا الاربعة تحوي عقدة(ذرة) واحدة فقط , و يمكن التأكد ان حجم كل هذه الخلايا متساوي تماماً

ولاحظ انه كما قلنا سابقا ان كل خلية تكرر نفسها بحيث تملأ كامل الفضاء وبحيث لا تتداخل مع نفسها ولا تترك اي فراغ.

وبالمثل في حالة شبكة ثلاثية الابعاد:

مثلاً لنأخذ شبكة مكعبية بسيطة  SC   (simple cubic)

وهي شبكة مهمة جداً و تعد من أبسط الشبكات البلورية

نلاحظ أن هذه الشبكة مبنية من مكعب واحد صغير يكرر نفسه

في كامل الفراغ بحيث يشكل الشبكة و هذا المكعب  هو خلية الوحدة الاولية لهذه الشبكة.

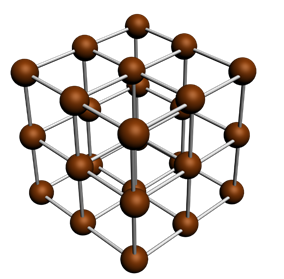شبكة مكعبية بسيطة

ملاحظة : قد لا يبدو المكعب الصغير(خلية الوحدة) انه يحوي ذرة واحدة فقط و ذلك لأنه لا يحوي ذرة واحدة (نقطة واحدة ) في داخله و انما يحوي ثمانية ذرات في زواياه

و لكن هنا كل ذرة تساهم في بناء ثمانية مكعبات اي ان مساهمة الذرة الواحدة في كل مكعب

هي  1/8 ذرة و بالتالي كل مكعب تساهم فيه (او يملك) ثمانية ذرات

 كل منها تسهم  بـ 1/8 

بالتالي لو جمعنا مساهمة  الذرات الثمانية نحصل على 1 ذرة في كل مكعب.

لتوضيح ذلك سنقوم بتحريك الشبكة و لكن بدون ان نحرك الذرات التي في الزوايا :

) قمنا بإزالة الذرات التي اصبحت خارج الشبكة

فقط للتوضيح )

  3- الخلية الاصطلاحية  unit cell (conventional unit cell

    هي خلية لا على التعيين نختاها بشكل عشوائي و لكن بشرط أن تكرار (او انتقال) هذه الخلية وفق مجموعة متجهات في شبكة برافيه يؤدي لملء كامل الفراغ بدون أي تداخل أو ترك فراغات

اي انه يمكننا ملء الفراغ بخلية ليست اولية (خلية وحدة اولية)

تسمى خلية وحدة اصطلاحية أو فقط خلية 

بشكل عام نختار الخلية الاصطلاحية بحيث تكون اكبر من الخلية الاولية و بحيث نحصل على التناظر المطلوب (المرغوب : الذي يعكس نوع خلية برافيه لهذه الخلية)

يوضح الشكل التالي خلية وحدة و خلية اصطلاحية لشبكة مكعبية متمركزة الجسمBCC

Body centered cubic

ويبين الشكل التالي ايضاً الخلية الاولية والاصطلاحية لشبكة مكعبية متمركزة الوجوه FCC

Face centered cubic

هنا أخترنا الخلية الاصطلاحية بشكل مكعب و هذا يعكس نوع النظام البلوري الذي تتبع له الشبكة و هي مكعبية في مثالنا

لاحظ في حالة الشبكة المكعبية البسيطة SC كانت الخلية الاولية على شكل مكعب و بالتالي لا حاجة للبحث عن خلية اصطلاحية حيث الخلية الاولية كانت بسيطة جداً على عكس الخلية الاولية في حالة BCC   و  FCC   حيث نلاحظ هنا ان الخلية الاولية تبدو أكثر تعقيداً وبالتالي من هنا جاءت الحاجة للبحث عن خلية أبسط للدراسة و الثمن كان الحصول على أكثر من ذرة ضمن هذه الخلية الجديدة و التي تم تسميتها الخلية الاصطلاحية ) غالباً نختار الخلية الاصطلاحية بحيث تملك محاور متعامدة x y zمما يسهل دراسة الجسم الصلب ) 

   4- خلية وينر - زايتس الاولية     wigner-seitz primitive cell

يمكن أن نختار  خلية الوحدة الأولية بحيث يكون لها نفس تناظر شبكة برافيه

حتى الأن أكثر خيار مستخدم هو خيار خلية وينر زايتس 

خلية وينر زايتس حول نقطة من الشبكة هي المنطقة من الفراغ التي تكون أقرب لهذه النقطة اكثر من قربها لأي نقطة أخرى من الشبكة

و نجد هنا أيضاً ان خلية وينر زايتس تملأ الفراغ أيضا أذا اجرينا انسحاب للخلية بدون أي تداخل أو ترك اي فراغ

خلية وينر زايتس هي خلية وحدة اولية.

- يبين الشكل التالي الخلايا الثلاث : الاولية و الاصطلاحية و خلية وينر زايتس لشبكة ذات بعدين :

يمكن البرهان بسهولة بطريقة هندسية انطلاقاً من ان خلية وينر زايتس اولية ان حجمها يساوي حجم الخلية الاولية :

يبين ذلكْ , الشكل التالي : فقط ضع كل قطعة مكانها

(اي نضع القطعة الملونة ذات الرقم 1 في الفراغ

الذي يحمل الرقم 1.......)

ونحصل على الخلية الاولية الاصلية

 طريقة تعيين خلية وينر زايتس بشكل بسيط :

نختار احدى الذرات ونمدد مستقيمات إلى أقرب الذرات لها ونأخذ اعمدة على منتصف هذه المستقيمات فيكون الحجم المحصور داخل هذه الأعمدة هو خلية وينر زايتس

تقديم : احمد القاسم

الشكر لمن ساهم بهذا العمل  Physics Group

---------------------------------------

لتحميل المقال كاملاً  pdf  انقر هنا

---------------------------------------

المراجع :

كتاب  Neil__W._Ashcroft Solid_State_Physics

كتب جامعة دمشق (الفيزياء العملية 7) لمجموعة من الدكاترة

كتاب فيزياء الجسم الصلب 1 _ جامعة دمشق

--------------

انتهى